
Welcome back to our series of articles sponsored by Intel – “Ask a Data Scientist.” Once a week you’ll see reader submitted questions of varying levels of technical detail answered by a practicing data scientist – sometimes by me and other times by an Intel data scientist. Think of this new insideBIGDATA feature as a valuable resource for you to get up to speed in this flourishing area of technology. If you have a big data question you’d like answered, please just enter a comment below, or send an e-mail to me at: daniel@insidehpc.com. This week’s question is from a reader who wants an explanation of the “bias vs. variance tradeoff in statistical learning.”
Q: Explain the bias vs. variance tradeoff in statistical learning.
A: The bias-variance tradeoff is an important aspect of data science projects based on machine learning. To simplify the discussion, let me provide an explanation of the tradeoff that avoids mathematical equations.
To approximate reality, learning algorithm use mathematical or statistical models whose “error” can be split into two main components: reducible and irreducible error. Irreducible error or inherent uncertainty is associated with a natural variability in a system. On the other hand, reducible error, as the name suggests, can be and should be minimized further to maximize accuracy.
Reducible error can be further decomposed into “error due to squared bias” and “error due to variance.” The data scientist’s goal is to simultaneously reduce bias and variance as much as possible in order to obtain as accurate model as is feasible. However, there is a tradeoff to be made when selecting models of different flexibility or complexity and in selecting appropriate training sets to minimize these sources of error!
The error due to squared bias is the amount by which the expected model prediction differs from the true value or target, over the training data. Because of that very particular definition, I tend to think of bias as being introduced at model selection. Now, data scientists can repeat the model building process (through resampling) to obtain the average of prediction values. If these average prediction values are substantially different that the true value, bias will be high.
The error due to variance is the amount by which the prediction, over one training set, differs from the expected predicted value, over all the training sets. As with bias, you can repeat the entire model building process multiple times. To paraphrase Manning et al (2008), variance measures how inconsistent are the predictions from one another, over different training sets, not whether they are accurate or not.
Models that exhibit small variance and high bias underfit the truth target. Models that exhibit high variance and low bias overfit the truth target. Note that if your target truth is highly nonlinear, and you select a linear model to approximate it, then you’re introducing a bias resulting from the linear model’s inability to capture nonlinearity. In fact, your linear model is underfitting the nonlinear target function over the training set. Likewise, if your target truth is linear, and you select a nonlinear model to approximate it, then you’re introducing a bias resulting from the nonlinear model’s inability to be linear where it needs to be. In fact, the nonlinear model is overfitting the linear target function over the training set.
The “tradeoff” between bias and variance can be viewed in this manner – a learning algorithm with low bias must be “flexible” so that it can fit the data well. But if the learning algorithm is too flexible (for instance, too linear), it will fit each training data set differently, and hence have high variance. A key characteristic of many supervised learning methods is a built-in way to control the bias-variance tradeoff either automatically or by providing a special parameter that the data scientist can adjust.
When working to characterize the bias-variance tradeoff, you need to develop metrics for determining the accuracy of your model. There are two common metrics used in machine learning: training error and test error. As an example, for linear regression models you can calculate the Mean Square Error (MSE) for the different data sets – training set to train the model (60-80% of the available data), and test set to check the accuracy of the model (40-20% of the available data). For completeness, there is an additional validation step after training. So a typical split is 50% training, 25% validation, and 25% test. The training set is for model fitting. The validation set is for estimating the prediction error so you can choose the appropriate model. And the test set is used to assess the model (and its error) once the model is chosen.
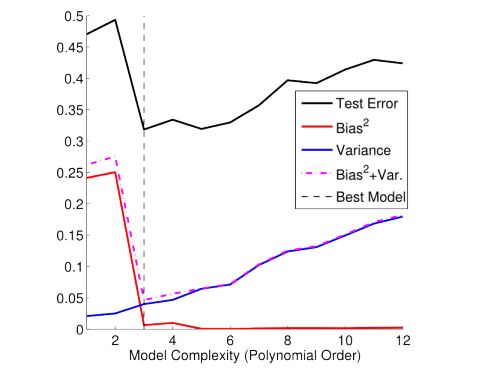
In the figure below, we see a plot of the model’s performance using prediction capability on the vertical axis as a function of model complexity on the horizontal axis. Here, we depict the case where we use a number of different orders of polynomial functions to approximate the target function. Shown in the figure are the calculated square bias, variance, and error on the test set for each of the estimator functions.
We see that as the model complexity increases, the variance slowly increases and the squared bias decreases. This points to the tradeoff between bias and variance due to model complexity, i.e. models that are too complex tend to have high variance and low bias, while models that are too simple will tend to have high bias and low variance. The best model will have both low bias and low variance. For a more detailed treatment of this example (along with the mathematics behind it!), please refer to a useful post on the The Clever Machine blog.
Managing the bias-variance tradeoff is one great example of how experienced data scientists serve an integral part of an analytics-driven business’ capability arsenal. Knowledge, experience and finesse is required to solve business problems. To learn more about managing bias-variance tradeoffs, I suggest the following readings:
- Geman, Stuart, Elie Bienenstock, and René Doursat. “Neural networks and the bias/variance dilemma.” Neural Computation 4(1): 1-58. 1992.
- Manning, Raghavan, Schutze. Introduction to Information Retrieval, Cambridge, 2008. University Press. 496 pages. http://nlp.stanford.edu/IR-book/
- Hastie, Tibshirani and Friedman. The Elements of Statistical Learning (2nd edition), Springer-Verlag, 2009. 763 pages. http://statweb.stanford.edu/~tibs/ElemStatLearn/
- James, Whitten, Hastie, Tibshirani. An Introduction to Statistical Learning with Applications in R, Springer, 2013. 426 pages. http://www-bcf.usc.edu/~gareth/ISL/index.html
Data Scientist: Dr. Monica Martinez-Canales is a Principal Engineer at Intel Corporation. She directs Big Data Solutions efforts on architectural integration across the different layers of the End-to-End Analytics Solution Stack (Silicon, Internet of Things, Data Platform, Analytics Platform, and Vertical Solutions). Prior to joining the Big Data Solutions team, Monica led Strategic Initiatives in Validation Business Intelligence & Analytics programs within the Platform Engineering Group. Monica’s most recent work on dynamic risk-based resource allocation strategies, under schedule pressure and resource constraints, drove the completion of post-silicon validation of the 4th Generation CPU family of products.
Monica earned a Ph.D. in Computational and Applied Mathematics from Rice University in 1998. Monica’s doctoral work focused on mathematical and numerical convergence of finite element models of shallow water systems. Monica received a B.S. in Mathematics from Stanford University in 1992.





“if your target truth is linear, and you select a nonlinear model to approximate it, then you’re introducing a bias”. I don’t understand why it introduces bias and not variance. Anyone to explain?
The nonlinear model swallows the natural variability in the system too much (maybe completely), so overfitting the (observations from the) truth target. In other words: the nonlinear model is (highly) biased.
A simple and extreme example: you fit datapoints/observations {(0,0),(1,1),(2,4)} produced by the linear system y=x+1+delta (where delta represents the natural variability, f.i. delta is Normal distributed), with the nonlinear model y = x^2+epsilon. You can see that the residuals from the truth system are completely gone when selecting the nonlinear modelfit (all observed epsilons are zero now), or to put it differently: the residuals are completely covered by the nonlinear modelfit. The nonlinear modelfit is completely biased to the observed random delta’s.
Bias is introduced by model selection. Note carefully that variance has two meanings in the above text: (1) the natural variability in the truth system (so not ‘introduced’) and (2) in the context of ‘error due to variance’: variance measures how inconsistent are the PREDICTIONS from one another, over different training sets, not whether they are accurate or not
There is always going to be bias and variance in any real world model. However, when using a non linear method to approximate a linear truth, the variance would typically be expected to outweigh the bias, as most non linear methods are more flexible than linear.
Also, from the structure of the example paragraph, I would expect that the intention is to say, in this sentence, that variance is introduced, as opposed to bias. Otherwise the paragraph states that:
low variance, high bias indicates underfitting (sentence 1)
high variance, low bias indicates overfitting (sentence 2)
(implied) low variance, high bias indicates underfitting (sentences 3 and 4)
(implied) low variance, high bias indicates overfitting (! sentences 5 and 6)
The best explanation I have ever read on this topic. Thank you Dr. Monica.
I think that the second sentence in the 7th paragraph beginning with ‘tradeoff’ should read something like “But if the learning algorithm is too flexible (for instance, is too non-linear), it will fit each training data set differently, and hence have high variance.” As written it uses linear as an example of a very flexible algorithm.
Yeah, I was confused there too.
Is my understanding correct?
Bias is when we assume certain things about the training data (it’s shape for example) and we choose a model accordingly. But, then we get predictions far away from the exptected values and we realise that we did a mistake in certain assumptions of our training data? Is my understanding correct?
Not entirely. Note the phrase in the article, “error due to squared bias.” This is the squared difference between your model and the actual training data (a sample), whatever your model is, and whatever the training data is. You can construct a model by adding lots of polynomial terms until the model fits the training data perfectly, and this will drive the squared bias down to zero. Your model makes all kinds of assumptions, which you might describe as “bias,” about the population data. But that is not what “error due to squared bias” means. It is simply the squared difference between your model’s prediction and the actual data. In this example, error due to squared bias is driven down, but it almost certainly drives error due to variance up, because the squiggly polynomial probably does not fit the population data nearly as well as it fits your training data. It overfits the training data.
So “error due to squared bias” means differences between your model and observations (training data). “Error due to variance” means differences between multiple sets of training data.
When you say, “we get predictions far away from the exptected values and we realise that we did a mistake in certain assumptions of our training data,” this is where I think you’re being inaccurate. You could overfit the data of your first training set with a bunch of polynomials, and then when you apply that model to a second training set, the errors are large. But it is not because your model is “biased” in the terms being used here, but rather because the “variance” between the two training sets is high.
Here is an analogy. You deal 100 cards, and 51 are red. One model predicts that all cards will be red, because a (slim) majority so far has been red. Another model considers the suit of the cards, whether the value is even or odd, which card came just before, etc., and uses all of that information to predict whether the next card is red or black.
Assuming that the cards being dealt are from standard 52-card decks in truly random order, the first model will suffer from high error due to bias, and the second from high error due to variance. However I didn’t specifically state that the cards being dealt were in a random order. It’s possible that the more complex model was pretty accurate. It’s also possible that there is some kind of non-random order to the cards, but the first 100 cards were just a really lousy representation of that order, so the all-cards-are-red model would be better (and some other, as-yet-undetermined model would be even better).
So the only way to gauge whether a model suffers from high error due to bias or variance is to keep sampling, and testing the model, and see how it does over multiple training sets. That is (I think) the point of the article.
We are struggling to know what is best path to choose. Machine learning as part of data science are not heuristically model where approximation and assumptions are conflict causing modes.